Matriz

Matemática - Matriz

Matrizes

Uma matriz de ordem m x n é qualquer conjunto de m . n elementos dispostos em m linhas e n colunas.

Representação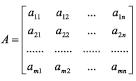

Cada elemento de uma matriz é localizado por dois índices: aij. O primeiro indica a linha, e o segundo, a coluna.

A matriz A pode ser representada abreviadamente por uma sentença matemática que indica a lei de formação para seus elementos.

A = (aij)mxn | lei de formação.

Ex.: (aij)2x3 | aij = i . j



Classificação das Matrizes

Em função dos valores de m e n, classifica-se a matriz A = (aij)mxn em:


Ex.: é uma matriz quadrada de ordem 3.

Numa matriz A = (aij)mxn quadrada de ordem n, os elementos aij com i = j constituem a diagonal principal. Os elementos aij com i + j = n + 1 formam a diagonal secundária.



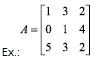
Tipos de Matrizes

Matriz Nula

É a matriz onde todos os elementos são nulos.


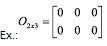
Matriz Oposta
Matriz oposta de uma matriz A = (aij)mxn é a matriz B = (bij)mxn tal que bij = -aij.




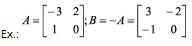
Operações com Matrizes


Matriz Identidade ou Matriz Unidade



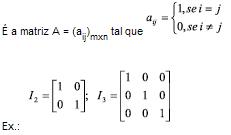
Matriz Transposta (At)

É a matriz que se obtém trocando ordenadamente as linhas pelas colunas da matriz dada.

Se B = (b_ij)_mxn é transposta de A = (a_ij)_mxn, então b_ij = a_ij.



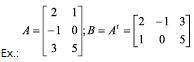
Matriz Diagonal

É uma matriz quadrada onde a_ij = 0, para i j, isto é, os elementos que não estão na diagonal principal são nulos.



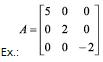
Matriz Simétrica

É uma matriz quadrada A tal que A^t = A, isto é, a^ij = a^ij para i j.




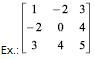
Matriz Anti-simétrica

É uma matriz quadrada A tal que A^t = -A , isto é, a_ij = -a_ij para i e j quaisquer.



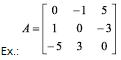
Operações com Matrizes

Igualdade de Matrizes

Duas matrizes A = (a_ij)_mxn e B = (b_ij)_mxn de mesma ordem, são iguais se, e somente se, a_ij = b_ij.



Propriedades da Igualdade

- Se A = B, então A^t = B^t

- (A^t)^t = A

Adição e subtração de Matrizes

A soma de duas matrizes A = (a_ij)_mxn e B = (b_ij)_mxn de mesma ordem é uma matriz C = (a_ij)_mxn tal que C = a_ij + b_ij.

A subtração de matrizes é dada pela sentença:

A – B = A + (– B )





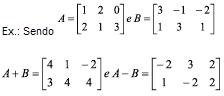
Propriedades da adição de Matrizes

a) A + B = B + A (COMUTATIVA)

b) (A + B) + C = A + (B + C) (ASSOCIATIVA)

c) A + 0 = 0 + A = A (ELEMENTO NEUTRO)

d) A + (-A) = (-A) + A = 0 (ELEMENTO OPOSTO)

e) (A + B)^T = A^T + B^T (TRANSPOSTA DA SOMA)

Produto de Matrizes

Produto de um Número Real por uma Matriz

Se é um número real, o produto desse número por uma matriz A = (a_ij)_mxn é uma matriz B = (b_ij)_mxn tal que b_ij = . a_ij



Propriedades do Produto de um Número por uma Matriz

Se A e B são matrizes de mesma ordem e e são números reais, valem as seguintes propriedades:

a) 1A = A

b) . (A + B) = A + B

c) . (b . A) = ( . b) . A

d) ( + b) . A = . A + b . A

e) ( . A)^T = . A^T

Produto de Matrizes

Dadas duas matrizes A = (a_ij)_mxn e B = (b_ij)_mxn, o produto da matriz A pela matriz B, nesta ordem, somente será possível quando o número de colunas da matriz A for igual ao número de linhas da matriz B.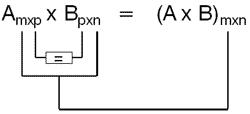



A matriz produto (A x B)_mxn terá número de linhas de A e número de colunas de B.

Os elementos da matriz produto são obtidos multiplicando-se cada elemento das linhas da matriz A pelo correspondente elemento das colunas da matriz B e adicionando os produtos obtidos.

Propriedades do Produto de Matrizes
Sendo A, B, C matrizes, e a um número real, e supondo as operações abaixo possíveis, temos que:

a) A.(B.C) = (A.B).C (ASSOCIATIVA)

b) A.(B+C) = A.B + A.C (DISTRIBUTIVA À DIREITA)

c) (A+B).C = A.C+B.C (DISTRIBUTIVA À ESQUERDA)

d) 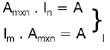I É A IDENTIDADE

e) (A . B) = A . (B) = . (A . B)

f) (A . B)T = BT . AT

Observações Importantes:

1.ª A multiplicação de matrizes não é comutativa, isto é, existem matrizes A e B tais que AB BA.

2.ª Na multiplicação de matrizes não vale o anulamento do produto, isto é, podemos ter A . B = 0 mesmo com A 0 e B 0.

3.ª Não vale também a simplificação, isto é, podemos ter AB = AC, mesmo com A 0 e B C.

Matriz Inversa

Uma matriz quadrada A de ordem n diz-se inversível ou não singular se, e somente se, existir uma matriz que indicamos por A^-1, denominada inversa de A, tal que: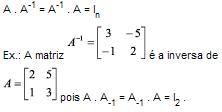

Condição de Existência da Matriz Inversa

Uma matriz quadrada A é inversível se, e somente se, o determinante de A for diferente de zero.

Elemento da Inversa b_ij de



Operação da Matriz Inversa

a) Calcule det A.

b) Determine a matriz dos co-fatores de A : A’.

c) Determine a matriz adjunta: = (A’)^t.

d) Aplique a fórmula .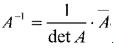


Aplicação



Equação Matricial

Sendo X, A e B matrizes quadradas de mesma ordem, demonstra-se que , se A e B admitem inversas, então:

X . A = B X = B . A-¹

A . X = B X = A^-1 . B